Standards-Based Grading Scales, Calculations, and Conversions

What is a Standards-Based Grading Scale?

Standards-Based Grading (SBG), also referred to as Mastery or Competency Grading, uses a different scale from the traditional 0-100 point grading scale. Many use a four-category scale to communicate a student’s level of mastery; however, this can vary depending on implementation.  

3 Things to Consider When Creating a Mastery Scale

Remember the Goal of Standards-Based Grading

SBG is meant to communicate how well a student understands a topic. The goal of SBG is not to reward students with a high score that includes late assignments, first attempts, and extra credit. Instead of scoring with an arbitrary number or letter, a mastery scale communicates the student’s current understanding of a topic. Each category of the standards-based grading scale should be easily identifiable by teachers, families, and students.

Make It a Conversation

There are many ways to use standards-based grading, and mastery scales can vary across learning communities. There is no standard way to use SBG, so having a conversation about what would best serve everyone involved is crucial. This communication will set up your school community for SBG success in the long run!

 

Avoid Adding Too Many or Ambiguous Categories

One of the benefits of a mastery scale is consistency across classrooms in a school community. With a traditional grading scale, teachers often have unique criteria for each grade. Since the criteria are specific to that teacher, understanding a student’s comprehension of a subject can be difficult. When transitioning to a Standards-Based approach, beware of using categories that are too difficult to distinguish. Setting your scale with clear and specific categories will easily communicate student performance.

Standards-Based Grading Conversion Methods

In some cases, converting a standards-based grade into a traditional letter grade may be necessary. While there is no “correct” method to accomplish this, a few conversion methods include the percentage and the Marzano methods.

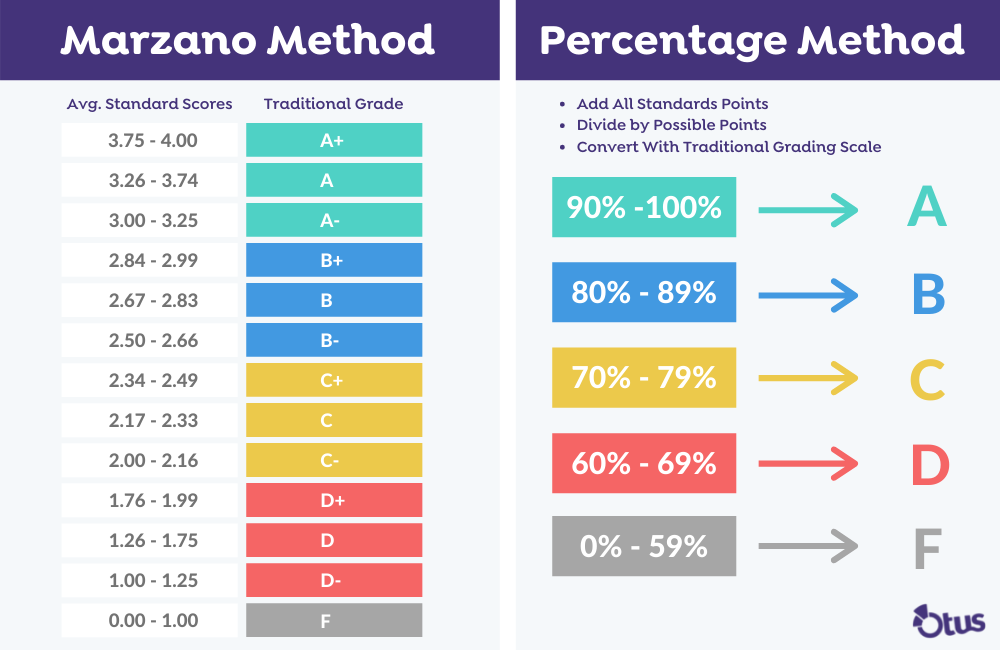
Marzano Method

Robert J. Marzano published the Marzano method in the book Formative Assessment & Standards-Based Grading. In this method, Marzano provides a chart with a 1-4 mastery scale. Using the average of a student’s SBG scores, you can quickly convert the standards grade into a traditional letter grade.

Percentage Method

The percentage method is intuitive and flexible for any grading scale. First, add the number of standard points the student earned. Then, divide that sum by the total number of points possible. Once you have that percentage, you can convert it using a traditional grading scale as pictured above. This method works for the common 1-4 scale as well as for 1-3 or 1-5 scales.

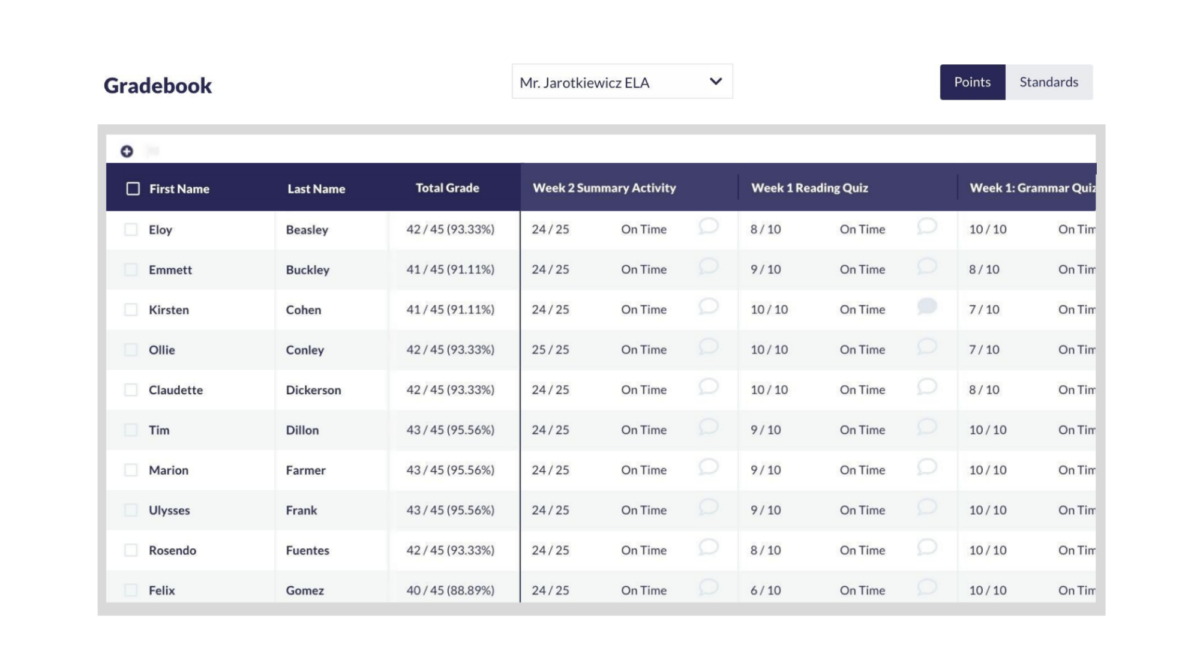
Otus Gradebook

The methods mentioned above are great ways to convert standards grades into traditional points grades, but what if you didn’t have to calculate a conversion at all? Using a standards-based grading tool like Otus, all assignments and assessments in Otus can be tied to standards. This flexibility allows for both points and standards-based grading, making the transition to SBG seamless and easier for teachers, students, and families.

How Is Standards-Based Grading Calculated?

Mastery can be calculated in several ways in a standards-based approach. The most popular calculation methods include decaying average, most recent score, highest score, mode, and mean. Each method differs in how it weighs recency versus consistency.

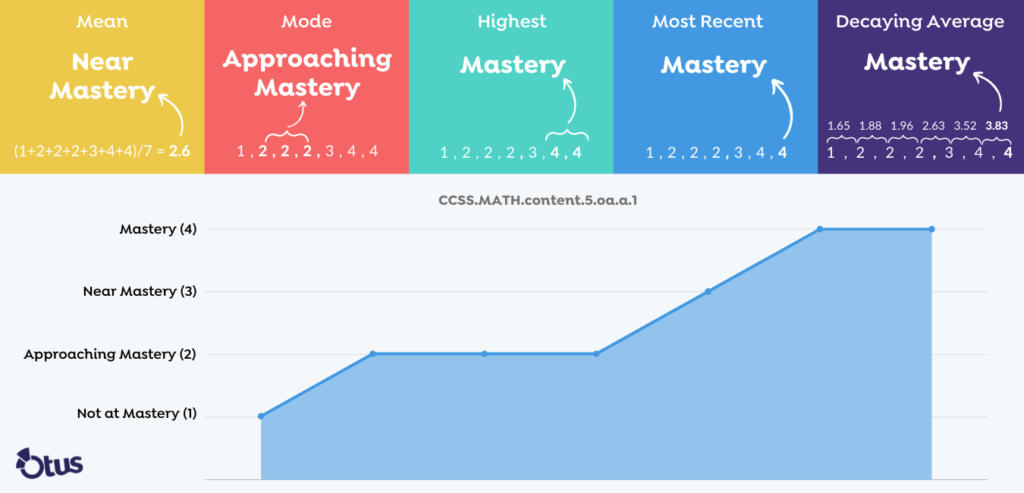
Mean

Calculating a student’s mastery using the mean is relatively straightforward. First, convert each level of your scale to a number. Often it will look something like this:

1 – Not at Mastery
2 – Approaching Mastery
3 – Near Mastry
4 – Mastery

Next, add all the student’s attempts at the standard and divide by the total number of attempts. Use standard rounding rules to round to the nearest whole, then convert back to the mastery level. Of all the calculation methods presented, using the mean most closely resembles a traditional grading approach. This method evenly weighs the first attempt and the last attempt.

Here are some examples:
(1 + 2 + 2 + 2 + 3 + 3 + 4 + 4) / 8 = 2.63 → Approaching Mastery
(2 + 3 + 4 + 3 + 4 + 4) / 6 = 3.33 → Near Mastery
(3 + 3 + 4 + 4 + 4) / 5 = 3.6 → Mastery

Mode

The mode is the grading scale level the student scored most frequently. This method, much like mean/average, does not consider the order of the attempts, only the frequency of results.

Here are some examples:
(Not at Mastery, Not at Mastery, Near Mastery, Mastery) → Not at Mastery
(Not at Mastery, Near Mastery, Near Mastery, Mastery) → Near Mastery
(Not at Mastery, Near Mastery, Approaching Mastery, Mastery, Mastery) — > Mastery

Highest

The “highest” calculation method is exactly what it sounds like. You use the highest level that the student ever achieved to calculate their total score. This method can safeguard against a lower recent score that might not accurately communicate the student’s full grasp of the standard. However, this can also work in the opposite direction and give a false positive for a student that doesn’t completely understand a standard.

Here are some examples:
(Not at Mastery, Approaching Mastery, Near Mastery, Near Mastery) → Near Mastery
(Not at Mastery, Not at Mastery, Near Mastery, Mastery, Near Mastery) → Mastery

Most Recent

This calculation method takes the student’s most recent score as their level of mastery. This method gives the most up-to-date view of the student’s proficiency but sacrifices the context of other recent scores.

Here are some examples:
(Near Mastery, Mastery, Mastery, Approaching Mastery) → Approaching Mastery
(Not at Mastery, Approaching Mastery, Mastery, Near Mastery) → Near Mastery
(Near Mastery, Near Mastery, Mastery) → Near Mastery

Decaying Average

This formula is calculated based on an average with more weight given to the most recent scores. The higher the decay rate, the more heavily recent assessments are weighed.

For example, if there are two assessments, the most recent assessment gets 65% weight, and the first gets 35%. For each additional assessment, the sum of the previous score calculations decays by an additional 35%. If you have three assessments, the weighting would be 12% for the first assessment, 23% for the second assessment, and 65% for the third assessment.

The math behind the 65% decaying average works like this:

Let’s say you have four assessments that receive the following scores: 1, 2, 3, 4 (the last score being the most recent).

(1 × .35) + (2 × .65) = X (X × .35) + (3 × .65) = Y
(Y × .35) + (4 × .65) = Z (this being the current standard score) 3.48

An example:
A student receives scores 2, 3, and 4 (most recent) on a single standard. Using decaying average, the student receives a 3.5. The formula calculates to a 3.5275 and rounds down.

If a student receives a score of 2, 4, 4, the decaying average formula calculates to a 3.755, so it rounds up.